Introduction
I glanced at a digital clock one day and noticed the time was reflectively symmetric, meaning if you flip the time over a horizontal line that divides the time in half it gives you the same time back. It made me wonder how many times there are that exhibit this behavior. I could have thought about all the times and probably come up with a list of them, but that is actually a lot of work. It would be much simpler to just have python give me the answer.
Types of Symmetry
The two types of symmetry I was interested in were reflective and rotational symmetry. These are standard symmetry types, and easy to code, and about all I really cared about, so that’s why I chose them.
Reflection Symmetry
Reflection symmetry occurs when you flip an image over an axis and get the same image back. So in this case if we define our axis to cut the time in half, horizontally, along the midpoint, and get the same thing back we have reflection symmetry.
2-fold Rotational Symmetry (Cyclic Group of Order 2)
2-fold Rotational Symmetry (180 degree rotational symmetry) occurs when you rotate an object 180 degrees and you get the same image back. This type of symmetry is also called Cyclic Group 2 symmetry. In general, Cyclic Groups of Order n are a mathematical construct that is studied in Abstract Algebra, but we need not go into that. All we’re going to concern ourselves with here is rotating an object 180 degrees, which is a simple thing to imagine.
Strategy to Solve
Each number on a digital clock can be defined by a simple python list. Let’s look at a diagram of the number 8 to see the mapping I chose:
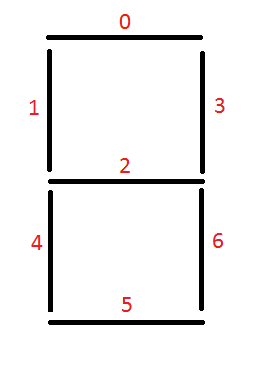
How I chose to map the number to a python list. Index of element in list is shown in red.
Using the diagram above we see that the following python list would represent a zero and eight, respectively:
zero = [1, 1, 0, 1, 1, 1, 1] eight = [1, 1, 1, 1, 1, 1, 1]
In our python code I define all the numbers in a dictionary as follows:
time_maps = {0: [1, 1, 0, 1, 1, 1, 1],
1: [0, 0, 0, 1, 0, 0, 1],
2: [1, 0, 1, 1, 1, 1, 0],
3: [1, 0, 1, 1, 0, 1, 1],
4: [0, 1, 1, 1, 0, 0, 1],
5: [1, 1, 1, 0, 0, 1, 1],
6: [1, 1, 1, 0, 1, 1, 1],
7: [1, 0, 0, 1, 0, 0, 1],
8: [1, 1, 1, 1, 1, 1, 1],
9: [1, 1, 1, 1, 0, 1, 1]}
Once the mapping is understood we can begin writing our program. Let’s start with reflection symmetry.
Reflection Symmetry Code Walkthrough
For reflection symmetry it’s pretty simple. If a time is going to be reflective then every number in the time must be reflective. So we begin by writing a function that tells us whether an individual number is reflective.
def individual_reflection_check(number):
""" check if a number is reflective """
tmp = list(time_maps[number])
tmp[0] = time_maps[number][5]
tmp[1] = time_maps[number][4]
tmp[2] = time_maps[number][2]
tmp[3] = time_maps[number][6]
tmp[4] = time_maps[number][1]
tmp[5] = time_maps[number][0]
tmp[6] = time_maps[number][3]
if tmp == time_maps[number]:
#print("%s is R." % number)
return True
else:
#print("%s is not R." % number)
return False
The mapping above is created by simply imagining where the lines on the digital clock shift to when you perform the reflection. It ends up being a simple shift of indices within the list that represents each number, which is what the previous function does. After the reflection is performed we check to see if some lists are the same, and if they are it means the time is reflective.
Let’s plug a couple numbers in to check our code:
print(individual_reflection_check(number=2)) print(individual_reflection_check(number=8)) >> False >> True
Next we take a look at whether or not a group of numbers together are reflective by simply making use of the function above multiple times.
def grouped_reflection_check(time):
"""
check if the time is reflective or not
:param time: a string like '3:45'
:return: None
"""
if re.search('[a-zA-Z]', time) is None:
# loop through time elements
for item in time:
if item != ':':
status = individual_reflection_check(int(item))
if status is True:
continue
else:
#print("The time %s is NOT R" % time)
return False
#print("The time %s is R" % time)
return True
else:
print("%s is not a valid time" % time)
Let’s check out if 1:11, 2:22, and 4:56 are reflective.
print(grouped_reflection_check(time='1:11')) print(grouped_reflection_check(time='2:22')) print(grouped_reflection_check(time='4:56')) >> True >> False >> False
The results were as expected. Now we want to know how many times are reflective among all the times. Here is the function I came up with that loops through all the times and gives us our answer:
def get_all_reflection_times():
""" the idea is all need to be reflective for it to work, let's get the list """
reflective_ls = []
counter = 0
for hr in range(1, 24):
for mini in range(0, 60):
if mini in range(0, 10):
mini = '0' + str(mini)
counter += 1
time = str(hr) + ":" + str(mini)
if grouped_reflection_check(time) is True:
reflective_ls.append(time)
print("There are %s times we checked." % counter)
print("There are %s total times that are reflective." % len(reflective_ls))
print("This gives %s percent of times that are reflective." % (100*float(len(reflective_ls))/float(counter)))
print("Here are the reflective times.")
for item in reflective_ls:
print(' ', item)
return reflective_ls
Running the function above gives the following output:
There are 1380 times we checked. There are 84 total times that are reflective. This gives 6.086956521739131 percent of times that are reflective. Here are the reflective times. 1:00 1:01 1:03 1:08 1:10 1:11 1:13 1:18 1:30 1:31 1:33 1:38 3:00 3:01 3:03 3:08 3:10 3:11 3:13 3:18 3:30 3:31 3:33 3:38 8:00 8:01 8:03 8:08 8:10 8:11 8:13 8:18 8:30 8:31 8:33 8:38 10:00 10:01 10:03 10:08 10:10 10:11 10:13 10:18 10:30 10:31 10:33 10:38 11:00 11:01 11:03 11:08 11:10 11:11 11:13 11:18 11:30 11:31 11:33 11:38 13:00 13:01 13:03 13:08 13:10 13:11 13:13 13:18 13:30 13:31 13:33 13:38 18:00 18:01 18:03 18:08 18:10 18:11 18:13 18:18 18:30 18:31 18:33 18:38
Good stuff! I thought there’d be more than 84 reflective times, but it’s a special property that not all numbers have, so it can’t be all that common. Next, let’s take a look at Rotational Symmetry.
Rotational Symmetry Code Walkthrough
Just like reflection symmetry we can imagine where the number vertices shift to when the rotation is performed and write up the following function that does the transformation:
def rotational_transformation(number):
""" perform the cyclic transformation on a number """
cycled = list(time_maps[number])
cycled[0] = time_maps[number][5]
cycled[1] = time_maps[number][6]
cycled[2] = time_maps[number][2]
cycled[3] = time_maps[number][4]
cycled[4] = time_maps[number][3]
cycled[5] = time_maps[number][0]
cycled[6] = time_maps[number][1]
return cycled
I wont bother with a print for the above code since all it’s doing is performing the rotation. The heavy lifter is the next python function that actually checks whether or not a time is rotationally symmetric or not. I came up with the following function to do this:
def grouped_rotation_check(time):
""" swap positions, ABCD -> DBCA
reflect DBCA
"""
if re.search('[a-zA-Z]', time) is None:
original_number = [time_maps[int(number)] for number in time if number != ':']
swapped = [int(time[i]) for i in range(len(time)-1, -1, -1) if time[i] != ':']
cycled_number = []
for number in swapped:
cn = rotational_transformation(number)
cycled_number.append(cn)
same = True
for og, cy in zip(original_number, cycled_number):
if og == cy:
continue
else:
same = False
break
return same
Let’s take a look at whether 1:11, 2:22, or 8:18 are symmetric with respect to our rotation.
grouped_rotation_check('1:11')
grouped_rotation_check('2:22')
grouped_rotation_check('8:18')
>> False
>> True
>> False
Interesting. Note that 1 is not rotationally symmetric because it “swaps sides”. Of course, 2 and 8 are rotationally symmetric. Next let’s write up a function just like we did with reflection symmetry that gathers all the rotationally symmetric times and reports on them:
def get_all_rotation_times():
""" report on all the rotationally symmetric times"""
cyclic_ls = []
counter = 0
for hr in range(1, 24):
for mini in range(0, 60):
if mini in range(0, 10):
mini = '0' + str(mini)
counter += 1
time = str(hr) + ":" + str(mini)
if grouped_rotation_check(time) is True:
cyclic_ls.append(time)
print("There are %s times we checked." % counter)
print("There are %s total times that are C2." % len(cyclic_ls))
print("This gives %s percent of times that are C2." % (100 * float(len(cyclic_ls)) / float(counter)))
print("Here are the C2 times.")
for item in cyclic_ls:
print(' ', item)
return cyclic_ls
Running the above function yields:
There are 1380 times we checked. There are 17 total times that are C2. This gives 1.2318840579710144 percent of times that are C2. Here are the C2 times. 2:02 2:22 2:52 5:05 5:25 5:55 6:09 6:29 6:59 8:08 8:28 8:58 9:06 9:26 9:56 20:02 22:22
From our results we see that significantly more times are reflective than rotationally symmetric, in fact nearly 4 times as many more. It looks like only the numbers 0, 2, 5, 8, and 9 yield rotationally symmetric times under certain combinations.
So then, how many times are both reflective and rotationally symmetric?
joint = list(set(reflective_ls).intersection(cyclic_ls))
print("Apparently there is only one reflective and C2 time, and it is %s." % joint[0])
>> Apparently there is only one reflective and C2 time, and it is 8:08.
Only one, and it’s 8:08. Savage! This is a special time indeed, for it also spells the name BOB. Hence, all BOB’s are reflective and rotationally symmetric.
Conclusion
This little project is boredom gone absolutely unchecked, but I just had to know the answer to the question. I hope that I can spare anyone else from using python for such an insipid use, and furthermore, I hope that the time 8:08 has a new special meaning for you!
Bonus Question
Create a histogram of the results above for each symmetry type.
Project Code
import re
"""
digital clock reflection symmetry and cyclic groups
_ _ _ _ _ _ _ _
| | | _| _| |_| |_ |_ | |_| |_|
|_| | |_ _| | _| |_| | |_| _|
0
1 3
2
4 6
5
number 0: [1, 1, 0, 1, 1, 1, 1]
number 1: [0, 0, 0, 1, 0, 0, 1]
number 2: [1, 0, 1, 1, 1, 1, 0]
number 3: [1, 0, 1, 1, 1, 1, 0]
number 4: [0, 1, 1, 1, 0, 0, 1]
number 5: [1, 1, 1, 0, 0, 1, 1]
number 6: [1, 1, 1, 0, 1, 1, 1]
number 7: [1, 0, 0, 1, 0, 0, 1]
number 8: [1, 1, 1, 1, 1, 1, 1]
number 9: [1, 1, 1, 1, 0, 1, 1]
the purpose of this program is to analyze reflection symmetry and cyclic groups of digital clocks
reflection symmetry:
R: horizontal reflection
example:
6:09 has reflection symmetry because flipping gives 6:09 back
cyclic groups:
Cn: 360 degrees / n
C1: 360 degrees
C2: 180 degrees
C3: 120 degrees
C4: 90 degrees
example:
3:03 has C2 symmetry because upon rotation we get 3:03 back
"""
time_maps = {0: [1, 1, 0, 1, 1, 1, 1],
1: [0, 0, 0, 1, 0, 0, 1],
2: [1, 0, 1, 1, 1, 1, 0],
3: [1, 0, 1, 1, 0, 1, 1],
4: [0, 1, 1, 1, 0, 0, 1],
5: [1, 1, 1, 0, 0, 1, 1],
6: [1, 1, 1, 0, 1, 1, 1],
7: [1, 0, 0, 1, 0, 0, 1],
8: [1, 1, 1, 1, 1, 1, 1],
9: [1, 1, 1, 1, 0, 1, 1]}
def individual_reflection_check(number):
"""
:param number: the number we are analyzing
:return: True/False value telling if symmetric
"""
tmp = list(time_maps[number])
tmp[0] = time_maps[number][5]
tmp[1] = time_maps[number][4]
tmp[2] = time_maps[number][2]
tmp[3] = time_maps[number][6]
tmp[4] = time_maps[number][1]
tmp[5] = time_maps[number][0]
tmp[6] = time_maps[number][3]
if tmp == time_maps[number]:
#print("%s is R." % number)
return True
else:
#print("%s is not R." % number)
return False
def grouped_reflection_check(time):
"""
format needs to be HR:MN ex: 3:45 (no reason for a trailing 0)
:param time:
:return:
"""
if re.search('[a-zA-Z]', time) is None:
# loop through time elements
for item in time:
if item != ':':
status = individual_reflection_check(int(item))
if status is True:
continue
else:
#print("The time %s is NOT R" % time)
return False
#print("The time %s is R" % time)
return True
else:
print("%s is not a valid time" % time)
def get_all_reflection_times():
""" the idea is all need to be reflective for it to work, let's get the list """
reflective_ls = []
counter = 0
for hr in range(1, 13):
for mini in range(0, 60):
if mini in range(0, 10):
mini = '0' + str(mini)
counter += 1
time = str(hr) + ":" + str(mini)
if grouped_reflection_check(time) is True:
reflective_ls.append(time)
print("There are %s times we checked." % counter)
print("There are %s total times that are reflective." % len(reflective_ls))
print("This gives %s percent of times that are reflective." % (100*float(len(reflective_ls))/float(counter)))
print("Here are the reflective times.")
for item in reflective_ls:
print(' ', item)
return reflective_ls
def rotational_transformation(number):
""" perform the cyclic transformation on a number """
cycled = list(time_maps[number])
cycled[0] = time_maps[number][5]
cycled[1] = time_maps[number][6]
cycled[2] = time_maps[number][2]
cycled[3] = time_maps[number][4]
cycled[4] = time_maps[number][3]
cycled[5] = time_maps[number][0]
cycled[6] = time_maps[number][1]
return cycled
def grouped_rotation_check(time):
""" swap positions, ABCD -> DBCA
reflect DBCA
"""
if re.search('[a-zA-Z]', time) is None:
original_number = [time_maps[int(number)] for number in time if number != ':']
swapped = [int(time[i]) for i in range(len(time)-1, -1, -1) if time[i] != ':']
cycled_number = []
for number in swapped:
cn = rotational_transformation(number)
cycled_number.append(cn)
same = True
for og, cy in zip(original_number, cycled_number):
if og == cy:
continue
else:
same = False
break
return same
def get_all_rotation_times():
""" report on all the rotationally symmetric times"""
cyclic_ls = []
counter = 0
for hr in range(1, 13):
for mini in range(0, 60):
if mini in range(0, 10):
mini = '0' + str(mini)
counter += 1
time = str(hr) + ":" + str(mini)
if grouped_rotation_check(time) is True:
cyclic_ls.append(time)
print("There are %s times we checked." % counter)
print("There are %s total times that are C2." % len(cyclic_ls))
print("This gives %s percent of times that are C2." % (100 * float(len(cyclic_ls)) / float(counter)))
print("Here are the C2 times.")
for item in cyclic_ls:
print(' ', item)
return cyclic_ls
if __name__ == "__main__":
reflective_ls = get_all_reflection_times()
cyclic_ls = get_all_rotation_times()
joint = list(set(reflective_ls).intersection(cyclic_ls))
print("Apparently there is only one reflective and C2 time, and it is %s." % joint[0])
Leave a Reply