Introduction
I’ve been teaching long enough now to know that, when it comes to fractions, my students tend to be very apprehensive toward working with them. As a result, I put this short guide together that my students could reference when they start working with fractions.
Requirements
- Know how to add, subtract, multiply, and divide numbers.
- Know how to find the greatest common factor (GCF) of two integers.
A quick review
First, I’m going to start with something super easy. It’s so easy even little kids can do it (literally). Let’s take a look at five plus five.
![]()
When we add five plus five we might not think we’re adding fractions, but in actuality both numbers can be thought of as having a common denominator of 1 as can be seen here:
![]()
When we sum integers together we ignore the fact that they have a denominator at all (because you know any number divided by 1 is itself). In fact, that’s how integers are defined, and it’s specifically why integers are a subset of the rational numbers. Integers are numbers divided by 1, whereas rational numbers can have any denominator they like except for 0.
You’re probably already aware of all that, but it’s good to double check. Now let’s introduce a situation where the denominator is no longer 1.
![Rendered by QuickLaTeX.com \[ \frac{5}{6} - \frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3} \cdot \frac{\color{red} \cancel{2}}{\color{red} \cancel{2}} = \frac{2}{3} \]](https://mathcodelife.com/wp-content/ql-cache/quicklatex.com-aa68b9542f8ec1c91c8307817567e700_l3.png)
As we can see, since the denominators are the same for the two fractions being subtracted we can simply subtract in the numerator over the common denominator. We then cancel out like terms once the subtraction is done.
Finally, let’s look at an example of combining fractions that have different denominators by using the greatest common factor.
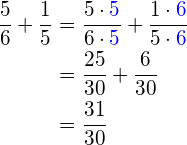
Since the GCF of 5 and 6 is 30 we use that to get a common denominator for the fractions ![]() and
and ![]() . I color coded how that was done with blue. We just multiplied the numerator and denominator by
. I color coded how that was done with blue. We just multiplied the numerator and denominator by ![]() or
or ![]() in order to make the two fractions have the same denominator. Once the denominator is the same we simply add as usual.
in order to make the two fractions have the same denominator. Once the denominator is the same we simply add as usual.
Compound fractions at last
Now that the review is over let’s take a look at an example of our first compound fraction, but first, let’s define what a compound fraction is.
[ compound fraction ]
A fraction in which either the numerator or the denominator, or both, contain one or more fractions.
So a compound fraction might look like this:
![]()
or even something more complicated like this:
![Rendered by QuickLaTeX.com \[ \frac{\frac{1}{7}+\frac{21}{3}}{\frac{5}{\frac{2}{13}}} \]](https://mathcodelife.com/wp-content/ql-cache/quicklatex.com-9e75878c424acaf251474e2258b4deff_l3.png)
Now that we’ve finally seen what the compound fraction monsters look like, let’s start defeating them. First, let’s start working on a plan of attack. An important thing to do when learning a new topic is to break it down into bite-sized portions we can manage. If we don’t do this we might get overwhelmed by the problem.
The best way to do this is to view the problem in pieces. Let’s look at the first problem above and focus on the two pieces it has, which have been placed in boxes.
![]()
Do you notice the box around the denominator can be simplified? As a first step always be sure to simplify all fractions before doing anything else. After simplifying we have:
![]()
At some point in school I was taught a way to do the next step of these which I’ve always remembered. In order to show you I’ll bust out Microsoft Paint and draw some lines. Check it out:
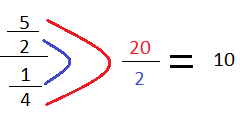
What the illustration shows is that we simply take the very top and very bottom and multiply them together and put the result in the numerator. We then take the middle terms and multiply them together and put the result in the denominator. This will always work. Every single time you can do this. Why? It’s simply another way of stating this formula which is taught in every beginner algebra class:
Uh oh, the problem changed!
A common thing students struggle with when learning elementary mathematics is doing problems that don’t look exactly like what they’ve done before. Let’s look at an example I’ve seen many students struggle with over the years:
![]()
Even though this is the same thing we’ve been doing all along, not every student is going to realize it. The key to doing this problem using the method I outlined above is to rewrite the problem like this ![]() . Once that’s done the problem is easy to solve:
. Once that’s done the problem is easy to solve:
![Rendered by QuickLaTeX.com \[ \frac{\frac{5}{8}}{\frac{2}{1}} = \frac{5 \cdot 1}{8 \cdot 2} = \frac{5}{16} \]](https://mathcodelife.com/wp-content/ql-cache/quicklatex.com-376cad34b32288e138301cd76541582e_l3.png)
Putting it all together
Let’s look at a final example that puts everything we’ve seen in one problem now.
![Rendered by QuickLaTeX.com \[ \frac{ \frac{1}{3} + \frac{1}{2} + \frac{7}{6} } { \frac{\frac{1}{2}}{\frac{1}{4}} } \]](https://mathcodelife.com/wp-content/ql-cache/quicklatex.com-10d52bd7e9e07b8be83ac3c016fb05be_l3.png)
Remember how we look at compound fractions without getting intimidated? — in pieces!
![Rendered by QuickLaTeX.com \[ \frac{ \boxed{\frac{1}{3} + \frac{1}{2} + \frac{7}{6}} } { \boxed{\frac{\frac{1}{2}}{\frac{1}{4}}} } \]](https://mathcodelife.com/wp-content/ql-cache/quicklatex.com-2f146634fca2f22d1a437e40ce6d915d_l3.png)
Let’s simplify the numerator first. To do this just find the GCF and add them together like we did in the review. So we get:
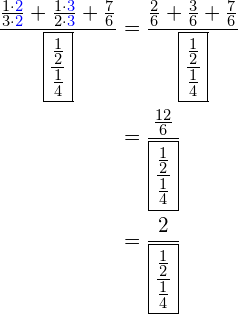
The last step is to look above to formula 1 (or our colorful red/blue line method) and simplify the denominator.
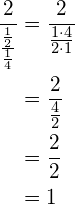
In the end, that terrifying compound fraction just turned out to be our friend, the number 1. This is a good lesson to end on: despite what the compound fraction looks like, always remember that ultimately every compound fraction is just a number.
Conclusion
My biggest hope here is that you’ll have more confidence when working with fractions. As you learn math you’ll be seeing a lot of new concepts, and many of them will require working with fractions, for example rational functions are a great example of this.
You don’t want the challenge of learning a new concept to be made even more difficult by not knowing how to work with fractions either. Keep this page as a reference, and come back to it whenever you get stuck — I hope it helps!
Bonus Questions
Simplify and leave the answer as a fraction if applicable (don’t write decimals).
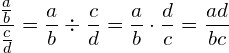
Leave a Reply