Some Thoughts
I think it goes without saying that writing a mathematical proof can be quite a challenge. Of course, with that challenge also comes great reward. A professor of mine once told me he liked to start off each morning with a cup of coffee and some problems from linear algebra. I imagine my professor sitting there working on problems that are either too easy or too difficult for him; the most difficult among them spawning countless papers containing unintelligible scribbles that only make sense to him. These scribbles will eventually lead him to the solution, or simply another dead end. Of course, most will be dead ends. In those scribbles I see genius and humanity. I see struggle and triumph. I see the essence of what mathematics really is.
The thing most people forget when they read a proof, and it isn’t even mentioned in school, is that the actual work required to generate the proof is not reflected in the proof. Most often the proof itself is sterile, lacking any humanity, and is a rather cold device. Students are expected to read a problem and generate a proof, leaving all their true work behind. They are to turn in only as many sheets of paper as the bare minimum assumptions will fit on; each line being absolutely required and tersely justified.
I think mathematics professors should put more emphasis on the attempts students make to find their solution. They should cherish the fact that students spent their nights struggling to find a solution, and never find it. They should provide nudges and hints; breadcrumbs that lead to the desired result. Mathematics to outsiders can appear as an enterprise only geniuses partake in, but that is not quite so. Most of the people I know were just regular people who enjoyed math.
Of course, that’s just my opinion. What I’d rather do instead of share an opinion is take some constructive steps toward helping you write better proofs. Here are five tips I put together that might help.
Five Tips for Writing Proofs
-
Find a good place to work, clear your mind, and focus. Eliminate distractions! For any creative endeavor the quickest way to not make progress is by being in an environment that’s not conducive to creation. If your creative space looks like a cup of tea and Mozart, then do that; or if it looks like two red bulls and Disturbed, then do that. Either way, do what allows you to turn blank paper into one filled with glorious work.
-
Understand the assumptions given by problem. This one can be tricky, and you really have to consider the setting of the problem you’re trying to solve. If it’s a routine homework assignment where you’re learning a new topic, then it’s usually counter-productive for the author of the problem to trick you with unnecessary assumptions. In this case read all of the assumptions carefully, and think about how you can use them to guide the creation of your proof. If it’s a math competition they could insert erroneous assumptions to try and throw you off course. If you’re clever then you’ll see the assumption(s) as unnecessary, and perhaps write your proof without using it. Either way, if you don’t understand the assumptions then you most likely wont be able to make any progress on the proof.
-
Use inductive reasoning and try to generalize the results. Proof by induction is often one of the first proof techniques taught in mathematical logic courses in an attempt to bridge the gap between computational mathematics and theoretical mathematics. The heuristics that go into developing those proofs can still serve you while exploring other proofs that won’t involve induction.
-
Develop the structure of your proof. The structure of your proof, in most cases, will be as follows. At the beginning of your proof write down the assumptions that you’re using in your proof. In many cases this will simply be the assumptions that were given to you, but you’ll often use other well known mathematical results at this stage also. The middle of your proof includes all the legwork where you systematically list out your computations and utilize the assumptions that lead you to the end of your proof. At the end of your proof you simply state why it’s self-evident at this point that what you’ve set out to prove has been done.
-
Read and re-read your proof again. This step is optional, but it’s akin to checking your work. Hopefully you’ve already sorted out any logical holes in your proof, but it’s quite possible that you’ve missed something. Go over all your assumptions and justify them one last time. Make sure you’ve used them correctly and that you have no typos in your proof. If you meant to write Let
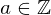, but instead wrote Let 
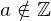, then the reader of your proof could be quite confused indeed. This could happen because when using LaTeX, or other similar languages, we tend to copy/paste a lot, and these errors become invisible to us while we’re working.
Conclusion
When you feel like you’ve hit a wall and you aren’t making any progress, remember that you’re not alone. Writing a proof can be a daunting task, and sometimes the only way to achieve success is to take a break and let your mind rest. You might just wake up with the answer you’ve been seeking!
Part 2
Next, let’s look at a proof I wrote on a very straightforward problem. I want to analyze the thought process behind it, and hopefully help an undergraduate freshman math major get started with writing their very own proofs. Just know that getting to the end of a proof can be time consuming, and challenging, but you’ll get there! Check out part two here!
Further Reading
[1] http://cheng.staff.shef.ac.uk/proofguide/proofguide.pdf
[2] http://zimmer.csufresno.edu/~larryc/proofs/proofs.html
Leave a Reply